O(N log N) Complexity - Similar to linear?

So I think I'm going to get buried for asking such a trivial question but I'm a little confused about something.

I have implemented quicksort in Java and C and I was doing some basic comparissons. The graph came out as two straight lines, with the C being 4ms faster than the Java counterpart over 100,000 random integers.

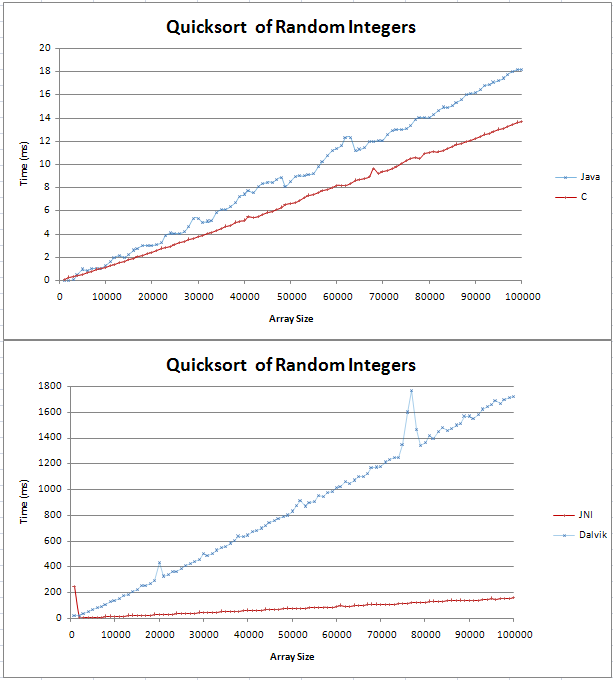
The code for my tests can be found here;

android-benchmarks

I wasn't sure what an (n log n) line would look like but I didn't think it would be straight. I just wanted to check that this is the expected result and that I shouldn't try to find an error in my code.

I stuck the formula into excel and for base 10 it seems to be a straight line with a kink at the start. Is this because the difference between log(n) and log(n+1) increases linearly?

Thanks,

Gav

Make the graph bigger and you'll see that O(n logn) isn't quite a straight line. But yes, it is pretty near to linear behaviour. To see why, just take the logarithm of a few very large numbers.

For example (base 10):

log(1000000) = 6
log(1000000000) = 9
…

So, to sort 1,000,000 numbers, an O(n logn) sorting adds a measly factor 6 (or just a bit more since most sorting algorithms will depend on base 2 logarithms). Not an awful lot.

In fact, this log factor is so extraordinarily small that for most orders of magnitude, established O(n logn) algorithms outperform linear time algorithms. A prominent example is the creation of a suffix array data structure.

A simple case has recently bitten me when I tried to improve a quicksort sorting of short strings by employing radix sort. Turns out, for short strings, this (linear time) radix sort was faster than quicksort, but there was a tipping point for still relatively short strings, since radix sort crucially depends on the length of the strings you sort.

FYI, quicksort is actually O(n^2), but with an average case of O(nlogn)

FYI, there is a pretty big difference between O(n) and O(nlogn). That's why it's not boundable by O(n) for any constant.

For a graphical demonstration see:

For even more fun in a similar vein, try plotting the time taken by n operations on the standard disjoint set data structure. It has been shown to be asymptotically n α(n) where α(n) is the inverse of the Ackermann function (though your usual algorithms textbook will probably only show a bound of n log log n or possibly n log* n). For any kind of number that you will be likely to encounter as the input size, α(n) ≤ 5 (and indeed log* n ≤ 5), although it does approach infinity asymptotically.

What I suppose you can learn from this is that while asymptotic complexity is a very useful tool for thinking about algorithms, it is not quite the same thing as practical efficiency.

1. Usually the O( n*log(n) ) algorithms have a 2-base logarithmic implementation.
2. For n = 1024, log(1024) = 10, so nlog(n) = 102410 = 10240 calculations, an increase by an order of magnitude.

So, O(n*log(n)) is similar to linear only for a small amount of data.

Tip: don't forget that quicksort behaves very well on random data and that it's not an O(n*log(n)) algorithm.

Any data can be plotted on a line if the axes are chosen correctly :-)

Wikipedia says Big-O is the worst case (i.e. f(x) is O(N) means f(x) is "bounded above" by N) https://en.wikipedia.org/wiki/Big_O_notation

Here is a nice set of graphs depicting the differences between various common functions: http://science.slc.edu/~jmarshall/courses/2002/spring/cs50/BigO/

The derivative of log(x) is 1/x. This is how quickly log(x) increases as x increases. It is not linear, though it may look like a straight line because it bends so slowly. When thinking of O(log(n)), I think of it as O(N^0+), i.e. the smallest power of N that is not a constant, since any positive constant power of N will overtake it eventually. It's not 100% accurate, so professors will get mad at you if you explain it that way.

The difference between logs of two different bases is a constant multiplier. Look up the formula for converting logs between two bases: (under "change of base" here: https://en.wikipedia.org/wiki/Logarithm) The trick is to treat k and b as constants.

In practice, there are normally going to be some hiccups in any data you plot. There will be differences in things outside your program (something swapping into the cpu ahead of your program, cache misses, etc). It takes many runs to get reliable data. Constants are the biggest enemy of trying to apply Big O notation to actual runtime. An O(N) algorithm with a high constant can be slower than an O(N^2) algorithm for small enough N.

log(N) is (very) roughly the number of digits in N. So, for the most part, there is little difference between log(n) and log(n+1)

Try plotting an actual linear line on top of it and you'll see the small increase. Note that the Y value at 50,0000 is less than the 1/2 Y value at 100,000.

It's there, but it's small. Which is why O(nlog(n)) is so good!